 It’s fine to compute means and statistically analyze ordinal data from rating scales.
It’s fine to compute means and statistically analyze ordinal data from rating scales.
But just because one rating is twice as high as another does not mean users are really twice as satisfied.
When we use rating scales in surveys, we’re translating intangible fuzzy attitudes about a topic into specific quantities.
Overall, how satisfied are you with your cell-phone service?
| Very Unsatisfied 1 |
2 | 3 | 4 | Very Satisfied 5 |
What does a response of a 4 really mean? How much faith should we put into this number?
Can we treat it the same as say as the temperature outside or the time it takes a user to create an invoice in accounting software? Are all numbers created equally or should we be more critical of how some numbers were obtained?
Levels of Measurment
For as long as we’ve been responding to these ubiquitous scales there have been debates about what we can and cannot do with them. One of the earliest and most influential papers on how we should classify the numbers we analyze comes from S.S. Stevens. In 1946 he wrote the seminal paper “On the theory of scales of measurement,[pdf]” where he put forth four levels of measurements:
Nominal: Numbers that are really just labels like a zip-code, a phone number, a checking account number or numbers on football uniforms. This one is easy to remember because nominal sounds like name.
Ordinal: Numbers that have an order like a runner’s finishing place in a race, the rank of a sports team and the values you get from rating scales used in surveys or questionnaires like the Single Ease Question.
We can’t say how the differences between the numbers correspond to the differences in the attribute they represent and we certainly can’t say the differences are all equal. Some teams may be separated by 1 win whereas others may have a 10 game gap. We can’t say for certain if the difference in satisfaction between a 4 and a 5 is the same as that between a 3 and a 4 on a rating scale.
Interval: If we can establish equal distances between ordinal numbers they become interval. The most common example is temperature in degrees Fahrenheit. The difference between 29 and 30 degrees on a thermometer is the same magnitude as the difference between 78 and 79 (I prefer the latter). Rating scales can be scaled to have equal intervals. For example, the Subjective Mental Effort Questionnaire (SMEQ) has values that correspond to the appropriate labels. You can see the distance between the numbers is equal, but the labels vary depending on how enough people interpreted their meaning (originally in Dutch).
You can drag the maroon slider up and down (apologies to iPad and iPhone users this is in Flash).
Ratio: Interval numbers that have a true or natural zero point are called ratio and represent the “highest” point in Stevens’ hierarchy. These would be task-times, reaction times or degrees Kelvin. In all cases 0 means the absence of something–time or heat in these examples. There has been some work in using ratio scales in usability data.
Levels dictate the appropriate analysis
Stevens’ didn’t create the classification just for taxonomic joy; instead he argued that only certain calculations are permissible with each level of data. In fact, he said that you can’t add, subtract much less compute a mean or standard deviations on anything less than interval data.
This restriction is a problem for many academics and applied researchers because rating scale data is at the heart of marketing, usability and much of social sciences research. If we cannot use means and standard deviations we also cannot use most statistical tests (which use means and standard deviations in their calculations). Even most non-parametric tests convert raw values to ranks (ordinal data) and then compute the mean or median.
Almost immediately after Stevens’ publication, counter arguments appeared which were critical of tethering statistical procedures to a number’s classification. A potent and now famous rebuttal[pdf] came from the eminent statistician Fredric Lord (who went on to help create things like the SAT at the Education Testing Service).
I can illustrate Lord’s criticism with Stevens’ rigid classification with a simple example.
7,6,4,2,9,10
Here are 6 high temperatures in Celsius from a Northeastern US city (interval data):
7,6,4,2,9,10
Here are 6 responses to the Likelihood to Recommend Question (ordinal data):
7,6,4,2,9,10
Now here are 6 numbers that came from the back of football jerseys (nominal data):
7,6,4,2,9,10
Can you tell the difference? The numbers don’t know where they came from and in fact they are all the same. You can compute the mean (6.33) and standard deviation (3.01) and perform statistical calculations regardless of where the numbers came from.
Lord in his satirical rebuttal showed how you could take means of football numbers to show that sophomores were leaving lower numbers to the freshman (a statistical analysis on Nominal data).
Despite the criticisms, Stevens’ classification system caught on and over 60 years later it is still taught in many introductory statistics courses. Some statistical packages still use Stevens’ language in guiding the appropriate test to use (see the figure below).
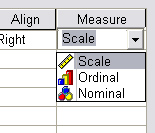
Figure 1: A screen shot from SPSS showing vestiges of Stevens’ hierarchy still in use.
You should care a little about where the numbers came from
You’re likely to encounter strong opinions on this matter but my recommendation is to go a head and compute means, standard deviations and statistical tests on ratings scales and other ordinal data. The large number of publications in the social sciences that use rating scales suggest I’m not alone despite the somewhat antiquated warnings. The numbers don’t know where they came from, however, this doesn’t mean we should ignore where they came from when we interpret them.
If the mean satisfaction score on Product A was 2 and 4 on Product B, this doesn’t necessarily mean that users are twice as satisfied on product B. Four is definitely twice two, but equating the mean response to actual levels of satisfaction is risky unless you can show that the feeling of satisfaction of a four is really twice as much as a two.
Beyond even satisfying the most stringent measurement theorist, there are other potential advantages to interval and ratio scales. A few years ago, Joe Dumas and I compared three single questions[pdf] which assessed the perceived usability of a task. One was ordinal (the SEQ), one interval (the SMEQ) and one ratio (a version of Usability Magnitude Estimation (UME) ).
We found that there was indeed some added benefit to the interval scaled SMEQ but it was only modest and it may have simply come from providing users with more response options. The SEQ has only 7 whereas the SMEQ had thousands of response options.
In applied research we are in most cases interested in determining which product or design generates higher scores, whether these be on satisfaction, usability or loyalty. The magnitude of the difference is also important–a 2 point difference is likely more noticeable to users than a ¼ point difference. But even if you were to commit the error and say that users were twice as satisfied on one product you’ve almost surely identified the better of two products even if the actual difference in satisfaction is more modest.


